Jedes Jahr das Gleiche beim Eurovision Song Contest: seltsame Auftritte, noch seltsamere Kostüme und zum Schluss die Vetternwirtschaft bei der Punktvergabe. Mir kam es schon immer ungerecht vor, dass kleine Länder wie San Marino oder Dänemark genauso viele Punkte vergeben dürfen wie Deutschland oder Italien. Ist dieses System vielleicht sogar Schuld daran, dass gefühlt immer nur Skandinavier, Ex-Ostblock- oder Balkanländer gewinnen?
Ich habe das einfach mal ausgerechnet. Dabei bin ich davon ausgegangen, dass die Punkte jedes Landes nach dessen Einwohnerzahl gewichtet werden sollten. Größere Länder bekommen dadurch mehr Gewicht als kleinere. 39 Länder durften beim ESC 2013 abstimmen, die mittlere Einwohnerzahl dieser 39 Staaten liegt bei 17,8 Millionen. Die Gewichtung funktioniert so: Ein Land, das doppelt so viele Einwohner hat wie der Durchschnittswert von 17,8 Millionen, darf auch doppelt so viele Punkte vergeben. Aus ursprünglich 12 Punkten für den Erstplatzierten werden so 24, 10 Punkte werden zu 20 und so weiter.
Ein Land hingegen, das halb so viele Bewohner hat wie der Mittelwert, darf nur halb so viele Punkte vergeben. Also 6 statt 12 für den Erstplatzierten, 5 statt 10 für den Zweiten und 0,5 statt 1 für den mit den wenigsten Punkten. Die Gewichtung verändert die Verteilung der Punkte, weil Giganten wie Russland (142 Mio. Einwohner) plötzlich nicht nur 58 Punkte vergeben (58 = 12+10+8+7+6+5+4+3+2+1), sondern acht mal so viele, nämlich 464. Deutschland (81 Mio.) kommt so auf 264 Punkte. Die Gesamtmenge der von allen 39 Ländern vergebenen Punkte bleibt jedoch unverändert – es wird ja schließlich nur anders gewichtet.
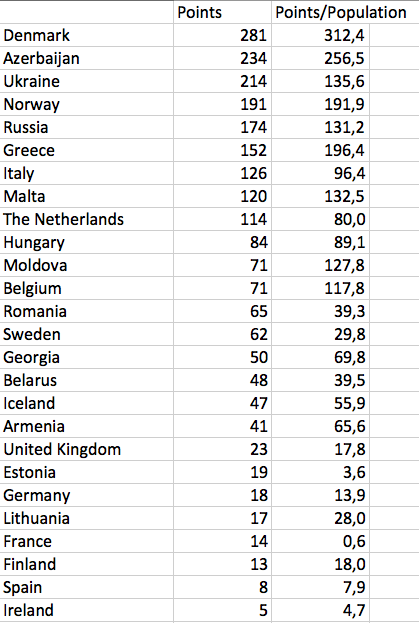
Und wer ist nun der gewichtete ESC-Sieger 2013? Es bleibt bei Dänemark – und ich muss gestehen, das hat mich überrascht. Das Siegerlied holt gewichtet mit 312,4 sogar noch mehr Punkte als die 281 aus der regulären Abstimmung. Den zweiten Platz sichert sich wiederum Aserbaidschan – mit gewichtet 256,5 statt 234 Punkten. Auf Platz drei aber landet nach der Neuberechnung Griechenland, das übrigens auch mein Favorit war. In der offiziellen ESC-Ranglisten erreichte es nur Rang sieben.
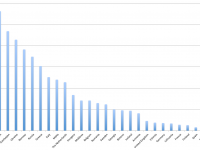
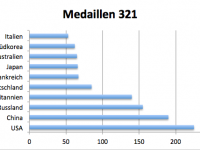
- Rangfolge laut der offiziellen Punktewertung – Dänemark gewinnt
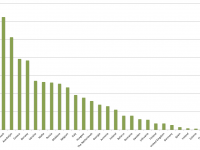
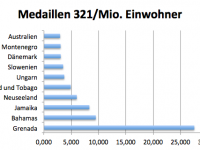
- Nach Einwohnerzahl gewichtete Rangfolge – auch hier gewinnt Dänemark
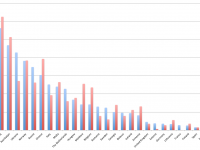
- Offizielles Ergebnis (blau) und Rangfolge nach Bevölkerung gewichtet (rot)
Copyright der Grafiken: Holger Dambeck
Aber ist eine solche Gewichtung wirklich fairer? Die Vetternwirtschaft wird tatsächlich verringert, denn kleine Länder, die sich gegenseitig Stimmen geben, beeinflussen die Gesamtabrechnung weniger stark. Doch nach wie vor dürfen Länder nicht für den eigenen Teilnehmer stimmen – und das wird für Kandidaten aus bevölkerungsreichen Staaten wie Russland, Deutschland oder Frankreich sogar zu einem echten Nachteil. Sie können dann von Vornherein nicht so viele Punkte einheimsen wie Dänemark oder Malta, weil die höher gewichteten Punkte aus ihrer Heimat ja nur für andere Länder zählen. Zudem muss die Einwohnerzahl nicht zwingend mit der Zahl der Anrufer aus einem Land korrelieren – eigentlich müsste man aber die tatsächlich abgegebenen Stimmen zählen wie bei einer demokratischen Wahl.
Das ganze Verfahren zeigt damit vor allem eines: Wie schwierig es ist, ein faires Wahlverfahren zu finden. Vielleicht ist das ja auch der eigentliche Sinn des Eurovision Song Contest.
Tabelle der Punktzahlen offiziell und gewichtet
Die Daten zum ESC 2013 habe ich von der Webseite escchat.com entnommen, die Einwohnerzahlen der Länder stammen aus dem CIA World Factbook. Wer gern selbst mit den Zahlen spielen will: Hier ist die Excel-Datei ESC Punkte gewichtet zum Download.