Archiv der Kategorie: Mathematik

Fußball-Bundesliga: Wie viele positive Corona-Tests kommen noch?

Veröffentlicht am von

Zwei Spieler und ein Betreuer mit dem Corona-Virus infiziert – diese Nachricht vom 1. FC Köln dürfte manchen überrascht haben. War das einfach nur großes Pech? Oder werden wir positive Tests jetzt öfters erleben, wenn die Bundesliga alle Teams regelmäßig untersucht?

Laufende Corona-Tests sind ein wichtiger Teil des Konzepts der Geisterspiele, mit dem die Bundesliga die derzeit unterbrochene Saison noch beenden will. In Liga 1 und 2 stehen noch neun Spieltage aus.

Nun gab es gleich zu Beginn der regelmäßigen Tests drei Positivfälle. Wie hoch ist eigentlich die Wahrscheinlichkeit dafür?

Bild: DFL

Ich habe ein wenig über diese Frage nachgedacht und festgestellt, dass das eine hübsche Fingerübung in Kombinatorik und Wahrscheinlichkeitsrechnung ist. Es wäre sicher auch ein schönes Thema für den Matheunterricht.

Das Ergebnis meiner Berechnungen hat mich selbst etwas überrascht: Sofern Infektionen unter Bundesliga-Fußballern genauso häufig sind wie in der Gesamtbevölkerung, liegt die Wahrscheinlichkeit für mindestens einen positiven Coronatest zwischen 0,4 und 0,9. Das gilt für einen einmaligen Test aller 36 Teams aus Liga 1 und 2. Ein ziemlich hoher Wert!

Wie habe ich das berechnet? Zunächst die Annahmen.

Anteil der infektiösen Menschen

Das Robert-Koch-Institut (RKI) beziffert die Zahl der täglichen Neuinfektion derzeit bei etwa 1000 (geschätzt über den Tag des Krankheitsbeginns, nicht über den Tag der Meldung!). Wir müssen aber von einer hohen Dunkelziffer ausgehen. Ich habe dabei zwei Varianten gewählt.

  • Entweder sind es in Wahrheit 5000 Neuinfizierte pro Tag. Bei den Tests würde also nur jeder fünfte Infizierte gefunden.
  • Oder es sind sogar 10.000 Neuinfizierte pro Tag. Bei den Tests würde dann sogar nur jeder zehnte Infizierte gefunden.

Ich habe angenommen, dass die Zahl der Neuinfizierten jeden Tag gleich bleibt. Damit ist der Reproduktionsfaktor gleich 1.

Weiterhin habe ich angenommen, dass das Virus im Hals der Infizierten an fünf aufeinanderfolgenden Tagen nachweisbar ist. Nur an diesen fünf Tagen kann der PCR-Test nach Abstrich im Rachen positiv ausfallen. Diese Anzahl der Tage könnte auch größer sein, das würde das Ergebnis der Berechnung verändern. Um einen solchen Effekt zumindest abschätzen zu können, habe ich auch ein Szenario mit zehn Tagen durchgerechnet.

Zunächst bleibe ich aber bei fünf Tagen.  Fünf Tage Infektiosität würde bedeuten: Pro Tag sind 5*5000 = 25.000 beziehungsweise 50.000 Menschen (=5*10.000) infektiös. Würde man an einem Tag alle 83 Millionen Bewohner Deutschlands testen, gäbe es 25.000 oder – bei Annahme der höheren Dunkelziffer – 50.000 positive Ergebnisse.

Dies entspricht 0,03 Prozent beziehungsweise 0,06 Prozent der Bevölkerung. Wer es etwas anschaulicher mag: Entweder ist einer von 3320 Menschen positiv oder einer von 1660.

Ist das Virus nicht fünf, sondern zehn Tage im Rachen nachweisbar, verdoppeln sich die Prozentwerte auf 0,06 beziehungsweise 0,12 Prozent der Bevölkerung, was 50.000 oder 100.000 infektiösen Menschen pro Tag entspricht. Dann wäre einer von 1660 oder einer von 830 Getesteten positiv.

Fasst man alle Szenarien zusammen, kommt man auf drei verschiedene Häufigkeiten von Infizierten mit nachweisbaren Viren im Rachen: Einer auf 830, 1660 oder 3320 Menschen.

Zahl der Tests bei Bundesliga-Teams

Laut den Angaben der DFL sollen von jeder Mannschaft nicht nur alle Spieler getestet werden – das sind meist 20 bis 30 -, sondern auch die Trainer, Mediziner, Physiotherapeuten und sonstigen Betreuer. Also alle, die in engem Kontakt zu den Spielern stehen. Dies sind laut DFL 50 Personen pro Team. Die beiden Bundesligen kommen zusammen auf 36 Teams. Wir reden hier also von 36*50 = 1800 Personen, die zugleich getestet werden.

Etwas Kombinatorik

Bei der folgenden Beispielrechnung gehe ich davon aus, dass im Durchschnitt eine von 1660 Personen im Rachen Corona-positiv ist. Ich teste alle 36 Liga-Teams – also 1800 Personen. Falls die Infektionsrate innerhalb der Teams genauso groß ist wie in der Gesamtbevölkerung, sollte im Durchschnitt etwas mehr als ein Test positiv ausfallen.

Ich möchte aber etwas genauer hinschauen: Wie groß ist die Wahrscheinlichkeit, dass alle 1800 Tests negativ sind? Und wie groß ist die Wahrscheinlichkeit, dass genau einer positiv ist? Oder mindestens einer?

Wer sich noch an Wahrscheinlichkeitsrechnung und Kombinatorik erinnert, weiß wahrscheinlich wie es weiter geht: Wir brauchen den Binomialkoeffizienten.

Fangen wir mit dem einfachsten Fall an: Alle 1800 Tests sollen negativ sein. Ich kann mir einen Corona-Test auch als Wurf mit einer Münze vorstellen. Die eine Seite der Münze steht für ein negatives Ergebnis, die andere für ein positives.

Bei einer Münze sind die Chancen normalerweise fifty-fifty. Die Corona-Test-Münze ist jedoch gezinkt: Nur mit p=1/1660 landet sie auf der Positiv-Seite, mit p=1659/1660 auf der Negativ-Seite.

Wenn ich 1800 Tests mache, werfe ich die Corona-Münze 1800 Mal hintereinander und sammle die Ergebnisse in einer Strichliste.

Wenn es keinen einzigen positiven Test gibt, also alle Tests negativ sind, ist die Wahrscheinlichkeit dafür:

p(0) = (1659/1660)^1800

p(0) = 0,338..

Wenn genau einer der 1800 Tests positiv sein soll, ist das Ergebnis

p(1) = (1659/1660)^1799 * (1/1660) * (1800 über 1)

p(1) = (1659/1660)^1799 * (1/1660) * 1800

p(1) = 0,367..

(1800 über 1) ist der Binomialkoeffizient. Er gibt an, wie viele verschiedene Möglichkeiten es gibt, dass von 1800 Würfen ein einziger positiv ist. Es sind genau 1800 verschiedene:

  • Wurf 1 ist positiv, alle anderen sind negativ,
  • Wurf 2 ist positiv, alle anderen sind negativ,
  • Wurf 3 ist positiv, alle anderen sind negativ,
  • …
  • bis Wurf 1800 ist positiv, alle anderen sind negativ.

Die allgemeine Formel lautet (n über k) = n!/( (n-k)! * k! ) – siehe https://de.wikipedia.org/wiki/Binomialkoeffizient

Wie groß ist die Wahrscheinlichkeit, dass genau 2 der 1800 Würfe ein positives Ergebnis haben? Auch das berechnen wir mit dem Binomialkoeffizienten – nun aber (1800 über 2):

p(2) = (1659/1660)^1798 * (1/1660)^2 * (1800 über 2)

p(2) = (1659/1660)^1798 * (1/1660)^2 * 1.619.100

p(2) = 0,199..

Auf diese Weise könnten wir für jede einzelne Anzahl positiver Tests die Wahrscheinlichkeit berechnen.

Ergebnisse für Tests mit 1800 Personen

Folgende Tabelle enthält die Wahrscheinlichkeiten dafür, dass 0, 1, 2, 3… Personen von 1800 getesteten positiv sind. Berechnet ist dies für die drei oben genannten Häufigkeiten infektiöser Menschen in der Gesamtbevölkerung (pi = 1/3320, pi = 1/1660, pi = 1/830).

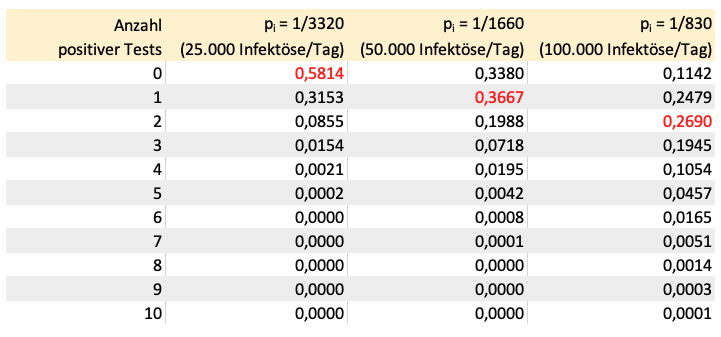
Wenn wir annehmen, dass die Corona-Infektionen in der Gruppe der 1800 Fußballer, Trainer und Betreuer genauso groß sind wie in der Gesamtbevölkerung, sind ein oder mehr positive Tests alles andere als unwahrscheinlich.

Schauen wir zuerst in die mittlere Spalte: Falls eine von 1660 Personen im Rachen nachweisbare Viren hat, ist die Wahrscheinlichkeit für genau einen positiven unter 1800 Tests nur minimal größer als für keinen einzigen positiven Test. Die Wahrscheinlichkeit für mindestens einen positiven Test ist mit p = 0,662.. deutlich größer als für 1800 negative Tests (p = 0,338).

Sind infektiöse Menschen doppelt so häufig (rechte Spalte), werden ausschließlich negative Tests mit p = 0,1142 schon relativ unwahrscheinlich. Mit jeweils p = 0,248 und p = 0,269 sind entweder genau ein Test oder zwei positiv. Die Wahrscheinlichkeit für mindestens einen positiven Test beträgt 0,8858. Und für mindestens zwei positive Tests immer noch mehr als 0,6.

Nur in der linken Spalte (pi = 1/3320) ist die Wahrscheinlichkeit für keinen einzigen negativen Test größer als 0,5 – aber auch hier sind ein oder mehr positive Tests mit p > 0,4 keine Seltenheit.

Fazit: Wir müssen bei den Tests der 1800 Teammitglieder häufig mit mindestens einem positiven Testergebnis rechnen.

Folgendes Diagramm zeigt die Verteilung der Wahrscheinlichkeiten in den drei Szenarien, die x-Achse zeigt die Anzahl positiver Tests, y steht für die Wahrscheinlichkeit.

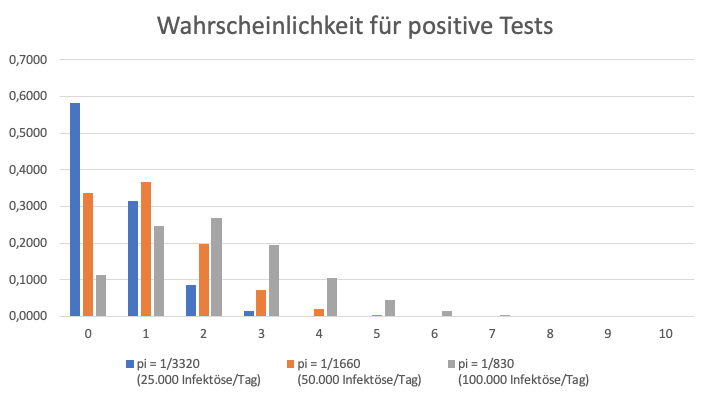
Kann das überhaupt stimmen?

Die Berechnung hat in meinen Augen zwei Schwächen. Zum einen ist unklar, ob man einfach so annehmen kann, dass Infektionen innerhalb der Fußballteams genauso häufig auftreten wie in der Gesamtbevölkerung. Hier könnte das Umfeld der Spieler eine Rolle spielen – aber auch die Tatsache, dass die Spieler in der Regel nicht mal 30 Jahre alt sind. Wir wissen bislang nicht genau, wie oft sich junge Erwachsene überhaupt infizieren.

Ein zweites, zumindest statistisches Problem ist die Häufung von Infektionen, wie wir sie im Fall des 1. FC Köln gesehen haben. Weil Spieler und Betreuer in kleinen Gruppen sehr eng zusammen sind, wird eine einzige Infektion sehr schnell an andere Teammitglieder weitergegeben. Die Infektion einer Einzelperson könnte daher eher selten sein, Infektionen treten womöglich häufiger als Cluster auf.

Es ist so ähnlich wie bei Familienmitgliedern, die in einem Haushalt zusammenwohnen. Auch hier bilden die Personen ein Cluster. Man kann sie nicht als Einzelpersonen betrachten, die voneinander unabhängig sind.

Wollte man beispielsweise anhand der positiven Tests unter Fußballteam-Mitgliedern die Häufigkeit positiver Tests abschätzen, müsste man womöglich die drei Personen eines Infektionsclusters zu einer Person (oder auch zu 1,5 Personen) zusammenfassen. Auf diese Weise vermeiden Epidemiologen Verzerrungen in ihren Daten.

Christian Drosten hat dies in einem seiner Podcasts für das Beispiel Gangelt (Landkreis Heinsberg) beschrieben. Dort wurden von einem Team des Virologen Hendrik Streeck viele Bewohner auf Antikörper getestet. Die Häufigkeit von Infektionen könnte überschätzt werden, falls der Faktor „wohnen gemeinsam in einem Haushalt“ nicht herausgerechnet wird.

Auch bei den Fußballern könnten die Infektionszahlen wegen des Clustereffekts verzerrt sein.

Fazit

Die simple Kalkulation zeigt, dass die DFL wohl mehr als nur einmal mit positiven Tests rechnen muss, sofern die simplen Annahmen der Kalkulation stimmen. Solange man auf Tests im Abstand von einer Woche schaut, kann man jeden dieser Tests mit 1800 Personen womöglich sogar als unabhängig von den vorherigen Tests betrachten – und damit als eine neue Stichprobe. Das gilt natürlich nur solange, wie die Zahl positiver Tests im Verhältnis zur Personenzahl klein bleibt, weil einmal Infizierte ja aller Voraussicht nach nicht noch mal infiziert werden können.

Wenn Spieler nun auch unter Körperkontakt trainieren und demnächst die eigentlichen Spiele beginnen, könnte aus einer Infektion, die ein Teammitglied einträgt, schnell ein Cluster von mehreren Infizierten werden. Wenn dies wiederholt geschieht, dürfte es schwierig werden mit dem regulären Beenden der Saison.

Es ist aber auch möglich, dass die positiven Tests beim 1. FC Köln tatsächlich nur großes Pech waren. Weil die Wahrscheinlichkeit für solche Infektionen in den Teams ein ganzes Stück kleiner ist als in den drei beschriebenen Szenarien.

ESC 2015: Beim Publikum hat Italien gewonnen

Veröffentlicht am von

Es war eine turbulente Nacht beim Eurovision Song Contest in Wien – und am Ende hieß der Sieger Schweden. Doch hätte allein das Publikum entschieden, wäre der Schwede Måns Zelmerlöw nur Dritter geworden. Platz zwei wäre an Russland gegangen – der Sieg aber an die drei Tenöre Il Volo aus Italien.

Viele ESC-Zuschauer wissen gar nicht, dass ihre Stimme nur zu 50 Prozent in die Wertung einfließt. Über die anderen 50 Prozent entscheidet eine fünfköpfige Jury, meist besetzt mit Musikexperten. In der deutschen Jury saß unter anderem Ferris MC von Deichkind. Solange Jury und Publikum ähnlich urteilen, hat das kaum Auswirkungen auf die Wertung. Sobald aber die Meinungen stark auseinandergehen, kann das passieren, was nun in Wien zu beobachten war: Italien, der klare Sieger des Televotes, geht leer aus.

ESC 2015 Saeulen Hätte allein das Publikumsvote gezählt, wäre Italien mit 365 Punkten unangefochten auf Platz 1 gelandet. Die folgenden Plätze wären an Russland (286 Punkte) und Schweden gegangen (272). Bei der offiziellen Gesamtpunktzahl hingegen ergab sich die bekannte Reihenfolge Schweden (365), Russland (303) und erst als Dritter Italien mit 292 Punkten.

Den Berechnungen hier liegt der übliche ESC-Modus zugrunde: Jedes der 40 Länder vergibt insgesamt 58 Punkte, der Erstplatzierte bekommt 12 Punkte, der zweite 10, der dritte 8, der vierte 7, … und der zehnte 1 Punkt.

Der Schwede Måns Zelmerlöw bekam den Grand Prix nur deshalb, weil er von den Experten aus den Jurys so hoch bewertet wurde. Die Details können Sie dem Diagramm oben und der folgenden Tabelle entnehmen:

ESC 2015 TabelleIm Vorjahr hatte bekanntlich Conchita Wurst den Eurovision Song Contest gewonnen – mit 290 Punkten. Der Sieg des Travestiekünstlers wäre aber noch viel deutlicher ausgefallen, hätten allein die Stimmen des Publikums gezählt – mehr dazu in meinem Text von vor einem Jahr. Immerhin wurde Conchita von den Jurys 2014 nicht um den Sieg gebracht. Denn auch bei ihnen lag Österreich ganz vorn, allerdings nur knapp.

Bei den drei Tenören von Il Volo aus Italien war das anders. Im Urteil der Jurys kam Italien insgesamt nur auf Rang 6 – und hatte so keine Chance, den Grand Prix zu gewinnen.

Wie unterschiedlich Publikum und Jury urteilten, zeigen die Beispiele Frankreich und Deutschland. Die Jury unseres Nachbarlandes wählte Il Volo auf Rang 15, die deutsche Jury sogar nur auf Rang 18. In beiden Fällen gleichbedeutend mit 0 Punkten, wenn die Juryentscheidung in Punkte ungerechnet worden wären.

Beim französischen und deutschen Televote kam Italien hingegen auf Platz 1, was 12 Punkten entspräche. Die offizielle Punktzahl wird wie folgt berechnet: Der Rang von Jury und der Rang Televote werden addiert. Das Land mit der niedrigsten Summe bekommt 12 Punkte, das zweite 10 und so weiter. So können sehr niedriger Rang und ein hoher Rang zusammen einen mittleren bis niedrigen Gesamtrang ergeben. Aus Deutschland bekam das italienische Trio schließlich nur 3 Punkte, aus Frankreich 6.

Vielleicht ein kleiner Trost für Deutschland: Bei den Jurys hätte die deutsche Sängerin Ann Sophie immerhin 24 Punkte eingeheimst – nur in der Gesamtwertung ging sie leer aus (0 Punkte).

Wer gern mit den ESC-Punkten spielen will: Hier ist die Datei ESC-2015-grand_final-full_results_holger mit den vollständigen Daten.

Wer hat eigentlich den ESC 2014 entschieden?

Veröffentlicht am von

Conchita Wurst hat den Eurovision Song Contest gewonnen. Der Travestiekünstler aus Österreich mit dem bürgerlichen Namen Tom Neuwirth bekam 290 Punkte. Platz 2 und 3 gingen an die The Common Linnets aus den Niederlanden (238 Punkte) und Sanna Nielsen aus Schweden (218 Punkte). Aber war das wirklich so ein klarer Sieg, wie ihn die Punktabstände suggerieren?

Viele Zuschauer wissen gar nicht, dass die Stimmvergabe eines Landes nur zum Teil übers Telefonvoting entschieden wird. In fast allen Ländern entscheidet eine fünfköpfige Jury mit – ihr Urteil und das Televote ergeben dann mit einer Gewichtung von je 50 Prozent das Gesamtvorting. Der ESC ist, wenn man so will, eine Mischung aus Demokratie und Expertokratie, denn die Jurys werden mit Vertretern aus der Musikbranche besetzt.

Natürlich sind Volkes Stimme und die Experten nicht immer einer Meinung. Beispiel Deutschland: Die Jury, in der unter anderem Jennifer Weist von der Band Jennifer Rostock und der Rapper Sido saßen, war von Conchita Wurst nur mäßig angetan. Im gemeinsamen Ranking der fünf Branchenvertreter kam sie nur auf Platz 11. Beim deutschen Televoting hingegen holte Conchita Wurst Platz 1. Beide Votes zusammen ergeben Platz 4 und damit 7 Punkte.

Da liegt natürlich die Frage nah: Wo hat Conchita Wurst eigentlich die meisten Unterstützer? Bei den Anrufern oder bei den Juryexperten? Und wie wäre der ESC ausgegangen, wenn allein das Televoting gezählt hätte? Und für wen hätten sich die Branchenvertreter aus den Jurys gemeinsam entschieden?

Die Ranglisten der Jurys und Telefonvotes sind auf der englischsprachigen ESC-Webseite komplett abrufbar – das Ganze lässt sich also leicht in Excel ausrechnen. Und das habe ich getan! 26 Titel waren im ESC-Finale, 37 Länder haben die Punkte vergeben. In Albanien und San Marino gab es kein Telefon-Vote, dort entschied allein eine Jury. In Georgien wiederum gab es nur ein Televoting. In den übrigen 34 Ländern entschieden Jury und Anrufer gemeinsam.

Den Berechnungen hier liegt der übliche ESC-Modus zugrunde: Jedes der 37 Länder vergibt insgesamt 58 Punkte, der Erstplatzierte bekommt 12 Punkte, der zweite 10, der dritte 8, der vierte 7, … und der zehnte 1 Punkt.

 

Hätten ausschließlich die Televotings beim ESC entschieden, wäre der Triumph von Conchita Wurst noch deutlicher ausgefallen. Sie hätte dann 306 Punkte erreicht – die Niederlande und Armenien würden mit 220 beziehungsweise 187 Punkte folgen. Schweden wäre auf Rang vier gelandet (173 Punkte) statt auf Platz 3 wie in der offiziellen Reihenfolge. Das gesamte Ranking finden Sie in der folgenden Tabelle (grüne Schrift):

ESC 2014

Hätten allein die Jurys über den ESC 2014 entschieden, wäre das Ergebnis zwar nicht anders, aber viel knapper ausgefallen – siehe rote Schrift. Österreich käme auf nur noch 214 Punkte, was aber immer noch für die Führung vor den Niederlanden (200 Punkte) und Schweden (199 Punkte) reicht.

Folgendes Diagramm zeigt die Platzierungen aus der Tabelle oben in Balkenform – nach den Modi Televote (grün), nur Jury rot) und Gesamt (grau). Gesamt entspricht der offiziellen ESC-Wertung. Die Länder sind nach dem Televote sortiert. Schön zu sehen ist, dass Länder wie Malta Aserbaidschan, Finnland und Norwegen zwar bei den Jurys gut punkteten – nicht aber bei den Anrufern.

ESC 2014 Punkte im Vergleich

Zum Schluss noch ein besonders spannender Blick auf die Punkte, die Österreich bekommen hat. Das Diagramm zeigt die von jedem Land an Österreich vergebenen Punkte in den Modi nur Jury und nur Televote (zum Vergrößern anklicken):

Conchita Wurst Jury vs. TelevoteBei vielen Ländern waren sich Anrufer und Experten weitgehend einig – die roten und blauen Balken sind ähnlich lang. Bei einem Drittel der Länder weicht Volkes Stimme jedoch deutlich vom Juryurteil ab – und zwar immer deutlich nach oben. Dazu gehören Portugal und Deutschland – aber auch viele ehemalige Ostblockstaaten wie Russland, Polen, Rumänien, Ungarn, Weißrussland und Polen.

Die eher geringe Toleranz in Osteuropa gegenüber Travestie und Homosexuellen spiegelt sich zwar im offiziellen Juryurteil wider – Österreich bekam dort kaum Punkte. Bei den Anrufern war Conchito Wurst hingegen populär. In Georgien und Armenien etwa holte sie  10 Punkte beim Televote, in Putins Russland immerhin 8 – von der Jury allein hätte das Lied keinen Punkt bekommen.

Vor diesem Hintergrund wirkt es besonders komisch, wenn nun russische Politiker vor dem Ende Europas warnen wie Wladimir Schirinowski. In Russland sammelte Conchita Wurst schließlich so viele Televotes ein, dass es auf Rang 3 (=8 Punkte) kam. Die namentlich bekannten russischen Jurymitglieder wählten Österreich auf Platz 11, weshalb es in der offiziellen russischen Gesamtwertung auf Platz 6 rutschte und nur 5 Punkte bekam.

Nachtrag: Wo die Fans „polnischer Folklore“ wohnen

Beim Spielen mit den Votes der Zuschauer und der Jurys ist mir noch das Kuriosium Polen aufgefallen. Ich fand den Beitrag „My Słowianie – We Are Slavic“ von Donatan und Cleo musikalisch eher dünn. Den Jury-Mitgliedern ging es offenbar ähnlich: Gerade mal in sechs Ländern schaffte er es im Expertenvote unter die Top-10 – und dabei auch nur auf die hinteren Ränge (blaue Balken im Diagramm unten). Die einzige Ausnahme bilden die deutschen Juroren, die Polen auf Platz 4 hievten, was 7 Punkten entsprechen würde, wenn allein das Voting der Jury über die Punkte entscheiden würde. (Diagramm zum Vergrößern anklicken)

ESC 2014 Polen

Ganz anders haben die Anrufer entschieden. In 12 Ländern schaffte es der polnische Song unter die ersten Top-3! Lag’s etwa an der üppigen Oberweite der Frau, die sich am Wäsche waschen mit der Hand versuchte? Hier die Länder, in denen Anrufer offenbar besonders auf „polnische Folklore“ stehen – sie liegen bis auf die Ukraine und Mazedonien sämtlich in Westeuropa:

Platz 1:
Ukraine, Irland, Norwegen, UK

Platz 2:
Island, Niederlande

Platz 3:
Deutschland, Italien, Österreich, Mazedonien, Frankreich, Schweden

Ähnlich auffällige Diskrepanzen gab es auch beim Beitrag aus der Schweiz. Das Lied punktete sehr oft bei den Zuschauern (rot), jedoch kaum bei den Jurys (blau).

ESC 2014 Schweiz

Wer einen Blick auf die Rohdaten werfen will – hier ist die Excel-Datei mit den Platzierungen aller Länder, aus denen sich die Punkte berechnen lassen: ESC 2014 Daten. Beim Juryurteil und dem Televote habe ich dem erstplatzierten Team 12 Punkte, dem zweiten 10, dem dritten 8, … und dem zehnten 1 Punkt gegeben. Zur Berechnung der offiziellen ESC-Wertung werden für jedes Land einzeln die Platzierungen von Jury und Televote addiert. Das Land mit der kleinsten Summe bekommt dann 12 Punkte, das mit der zweitkleinsten 10 und so weiter.  Ab Platz 11 gibt es 0 Punkte.

 

Die raffinierten Logik-Zwerge

Veröffentlicht am von

Das folgende Rätsel hat mir Ansbert Kneip vom Kindermagazin DeinSPIEGEL geschickt – man findet es in verschiedenen Variationen immer wieder. Ich finde es ziemlich schwer, von allein habe ich die Lösung nicht gefunden. Schaffen Sie’s?

In einer dunklen Höhle leben Logik-Zwerge, die entweder eine weiße oder eine schwarze Mütze aufhaben. Die Zwerge wissen nicht, wie viele von ihnen es gibt. Einmal im Jahr  dürfen sie die Höhle verlassen und bekommen eine Aufgabe gestellt. Können sie diese  lösen, sind sie frei. Misslingt die Lösung, müssen sie zurück in die Finsternis.

In diesem Jahr lautet die Aufgabe: Stellt euch nebeneinander auf, und zwar so, dass die Zwerge mit einer weißen Mütze auf der einen Seite stehen und die mit schwarzer Mütze auf der anderen. Dummerweise kann keiner der Zwerge die Farbe seiner eigenen Mütze sehen. Zudem dürfen sie weder miteinander reden noch sich auf sonstige Weise verständigen oder Hinweise geben, etwa mit der Hand oder den Augen. Sie dürfen auch nicht auf Tricks wie einen Spiegel zurückgreifen.

Das einzige, was die Logik-Zwerge nutzen dürfen, ist ihr scharfer Verstand. Wie können sie die Aufgabe lösen?

Lösungen gern per Mail an mich holger.dambeck AT googlemail.com. Viel Erfolg!

Mit Elfteln rechnen

Veröffentlicht am von

Letzte Woche hatte ich folgende Frage gestellt: Punkt Mitternacht stehen großer und kleiner Zeiger genau übereinander. Wie viel Zeit vergeht, bis das wieder der Fall ist?

Uhr 2 quer

Offensichtlich vergeht mehr als eine Stunde, denn erst kurz nach 1.00 Uhr überrundet der große den kleinen Zeiger. Man könnte die Aufgabe mit einem Gleichungssystem lösen, in dem die Zeit t die Unbekannte ist. Wir kennen die Position beider Zeiger um 0.00 Uhr – sie stehen beide auf der 12. Kurz nach 1.00 Uhr treffen sie sich wieder. Der große Zeiger hat dann exakt 360 Grad mehr zurückgelegt als der kleine Zeiger. Also gilt

vg * t – 360 Grad = vk * t

(Wobei vg und vt die Winkelgeschwindigkeit von großem bzw. kleinem Zeiger sind. vg = 360 Grad/Stunde, vk = 30 Grad/Stunde)

Diese Gleichung löst man nach t auf – das ist die Standardlösung.

Schöner finde ich jedoch die Folgende: Um 0.00 Uhr und um 12.00 Uhr stehen die Zeiger exakt übereinander. Zwischen 0.00 und 12.00 Uhr gibt es zehn Überholmanöver. Diese teilen die zwölf Stunden in elf gleich lange Zwischenräume ein, denn die Zeiger bewegen sich mit konstanter Geschwindigkeit. Der Abstand zwischen zwei Begegnungen ist deshalb 12/11 Stunden. Eine elftel Stunde entspricht etwa 5 Minuten und 27 Sekunden. Beim ersten Wiedertreffen der Zeiger nach Mitternacht ist es demnach 1:05:27 Uhr.

Noch ein Uhrenrätsel

Veröffentlicht am von

Mit der Frage nach dem Winkel zwischen großem und kleinem Zeiger um 15.10 Uhr habe ich letzte Woche so manchen aufs Glatteis geführt. Hier kommt noch ein Uhrenrätsel – und das ist noch eine ganze Ecke schwieriger, wie ich finde.

Uhr quer

Punkt Mitternacht stehen großer und kleiner Zeiger genau übereinander. Wie viel Zeit vergeht, bis das wieder der Fall ist? Anders formuliert: Wie spät ist es beim nächsten Rendezvous der Zeiger?

Lösungen bitte an holger.dambeck AT googlemail.com – diesmal geht es nicht um ein Buch, sondern nur um Ruhm und Ehre.

Es sind 35 Grad

Veröffentlicht am von

Die Lösung des gestrigen Uhrenrätsels war wohl doch nicht ganz so leicht. Ich hatte gefragt, in welchem Winkel die Zeiger einer Uhr um 15.10 Uhr zueinander stehen. In der ersten E-Mail, die ich bekam, stand 30 Grad. Und in der darauf folgenden auch. Leider stimmt das aber nicht.

Der Winkel ist ein Stückchen größer. Der große Zeiger steht um 15.10 Uhr auf der 2 des Ziffernblatts. Der Winkel bis zur 3 ist genau 30 Grad (=1/12 von 360 Grad). Doch der kleine Zeiger befindet sich um 15.10 Uhr nicht mehr genau über der 3. Er hat sich vielmehr in den zehn Minuten seit 15.00 Uhr ein kleines Stück weiterbewegt.

Aber um wie viel Grad? In 12 Stunden überstreicht der kleine Zeiger 360 Grad, also in einer Stunde 30 Grad. 10 Minuten sind ein Sechstel einer Stunde. In dieser Zeit bewegt sich der Zeiger um ein Sechstel von 30 Grad = 5 Grad. Der gesuchte Winkel zwischen den beiden Zeigern beträgt deshalb 35 Grad.

Die schnellste richtige Lösung kam via Twitter – ich nehme Kontakt zu dem Gewinner meines Buchs „Nullen machen Einsen groß“ auf. Nächste Woche folgt ein ziemlich raffiniertes Logikrätsel.

Ein Uhrenrätsel

Veröffentlicht am von

Ich habe mir vorgenommen, in meinem Blog regelmäßig kleine mathematische Rätsel zu stellen. Sie sollen nicht allzu schwer sein – aber manchmal könnte es auch anspruchsvoll werden wie zuletzt bei der Knobelei mit dem Fahrrad. Mal sehen, ob ich das einmal pro Woche hinbekomme. Beginnen möchte ich mit einer relativ leichten Aufgabe:

Die Zeiger der Uhr zeigen die Zeit 15.10 Uhr an. Wie groß ist der Winkel zwischen großem und kleinem Zeiger in diesem Moment?

Die Lösung gibt es morgen hier in meinem Blog.

Es gibt auch etwas zu gewinnen: Schicken Sie die Lösung an holger.dambeck AT googlemail.com – der schnellste Einsender bekommt ein Exemplar meines 2013 erschienenen Buches „Nullen machen Einsen groß“.

Viel Glück!

Heute Verkaufsstart für mein neues Buch

Veröffentlicht am von

Es geht endlich los: Heute, am 20. Juni, ist mein neues Buch „Nullen machen Einsen groß“ offiziell erschienen. Darin beschreibe ich Mathetricks aller Art – von Rechenkniffen bis zu richtigen Zauberkunststücken, die auf Mathematik beruhen. Einige kurze Auszüge werden demnächst auf SPIEGEL ONLINE publiziert.

An dieser Stelle möchte ich ein paar Fotos aus dem vierten Kapitel zeigen, in dem es um Krawattenknoten und Schnürsenkel geht. Es ist unglaublich, wie viele Möglichkeiten es gibt, Schnürsenkel einzufädeln. Ein paar davon sind auf den Fotos zu sehen. Die Fotos stammen von Oliver Mann – ein paar Eindrücke vom Fotoshooting gibt es hier.

Mein neues Buch ist da!

Veröffentlicht am von

Endlich ist es gedruckt – mein drittes populärwissenschaftliches Buch über Mathematik. In „Nullen machen Einsen groß“ geht es um mathematische Kniffe und Kunststücke aller Art. Natürlich sind Rechentricks dabei, aber auch geometrische Spielereien wie das Dritteln eines Winkels und richtige Zaubertricks mit Geburtstagen, Dominosteinen und Spielkarten, die Mathematik nutzen.

Nullen machen Einsen groß

Ich habe ein gutes Gefühl und glaube, dass es tatsächlich mein bisher bestes Buch ist. Es bietet eine bunte Mischung aus relativ leicht zu verstehenden Tricks, enthält aber auch Anspruchsvolleres wie etwa die kaum noch bekannte Trachtenberg-Schnellrechenmethode. Spannend ist sicher auch das Kapitel über Schnürsenkel und Krawattenknoten. Und wer gern knobelt, kann sich an insgesamt 45 Matherätseln ausprobieren.

Ich hoffe, das Buch kommt bei den Lesern ähnlich gut an wie „Je mehr Löcher, desto weniger Käse“. Das hat sich mehrere Wochen in den Top 20 der Bestsellerliste gehalten – und dorthin sollten es auch die Mathetricks schaffen 😉