Archiv des Autors: hdambeck

Auflösung des Mathe-Fahrrad-Rätsels

Veröffentlicht am von

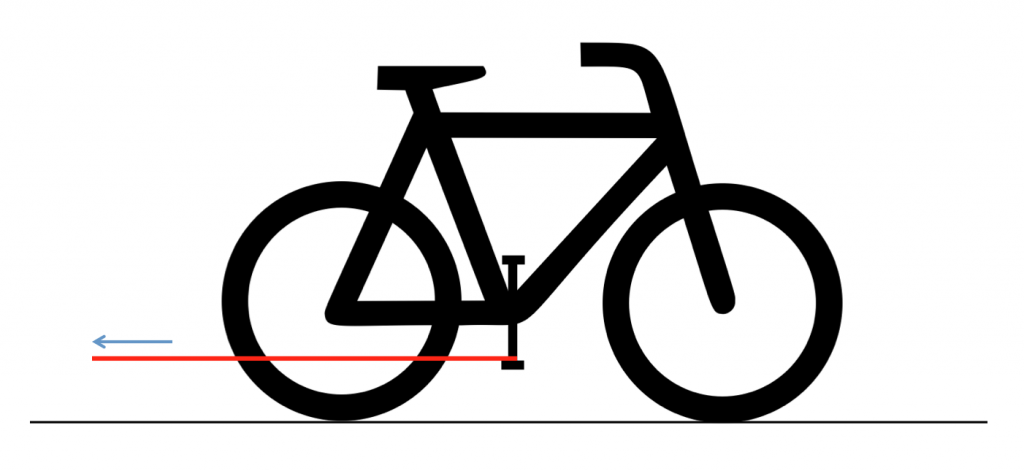
Vor lauter Weihnachtsstress bin ich gar nicht dazu gekommen, die Lösung des letzten Rätsels zu posten. Rollt das Rad ein Stück nach vorn? Bleibt es auf der Stelle stehen? Oder rollt es rückwärts?

Nehmen wir einfach mal an, das Rad hat eine Übersetzung von 1:1. Das bedeutet: Bei einer vollständigen Kurbelumdrehung dreht sich das Hinterrad eine vollständige Runde. Wir schauen uns nun in einem Gedankenexperiment an, was passiert, wenn ich die Pedale um einen sehr kleinen Winkel x drehe. Dann dreht sich logischerweise auch das Hinterrad um diesen Winkel x – die Übersetzung ist ja 1:1. Weil der Radius des Hinterrades größer ist als die Pedallänge, legt das Hinterrad im Moment des Ziehens an dem Seil ein größeres Wegstück nach vorn zurück als die Pedalspitze nach hinten.

Das Seil müsste länger werden, damit das überhaupt möglich ist. Aber ich ziehe ja an dem Seil. Das bedeutet: Das Rad bleibt auf der Stelle stehen, ich kann es durch Ziehen am Seil nicht nach vorn bewegen.

Die Übersetzung eines Rades ist sogar in der Regel größer als 1:1, das Laufrad bewegt sich also in jedem Fall ein größeres Stück nach vorn als die Pedalspitze zurück. Rückwärts rollen kann es nicht, weil ich durch die Ziehbewegung ja eine (nur minimale) Bewegung der Räder nach vorn auslöse, die dann vom straffen Seil gestoppt wird. Deshalb bleibt das Rad auf der Stelle stehen.

Raffiniert: Ein Mathematik- und Fahrrad-Rätsel

Veröffentlicht am von

Ich schreibe bei SPIEGEL ONLINE viel über Mathematik und Physik – aber auch über Fahrräder. Besonders freut es mich, wenn diese nicht gerade verwandten Themengebiete dann in einem Text gemeinsam auftauchen. So geschehen jüngst in dem Artikel über die Vor- und Nachteile der Reifengrößen 29 Zoll, 27,5 Zoll und und 26 Zoll bei Mountainbikes. Ein weiteres Beispiel ist der Text übers Freihändigfahren – ein selbst von Physikprofessoren oft falsch erklärtes Phänomen.

Nun kann ich Mathematik und Fahrräder ein weiteres mal zusammenbringen – und zwar in einem hübschen Rätsel, das ich in einem alten Buch von Martin Gardner entdeckt habe. Stellen wir uns ein Fixie vor, ein Rad mit nur einem Gang und starrer Nabe ohne Freilauf. Wenn ich auf einem Fixie sitze und rückwärts trete, fährt das Rad auch rückwärts.

Bild: public domain, Quelle: Wikipedia

Die Pedale stehen senkrecht zum Boden. Am unteren Pedal ist ein rotes Seil befestigt – siehe Zeichnung. Neben dem Rad steht jemand und stützt es mit einer Hand am Sattel, damit es nicht zur Seite umfällt. Eine zweite Person steht hinter dem Rad und beginnt, am roten Seil zu ziehen. Was passiert mit dem Rad, wenn wir annehmen, dass die Reibung zwischen Reifen und Straße so groß ist, dass die Räder weder durchdrehen können noch rutschen? Rollt das Rad ein Stück nach vorn? Bleibt es auf der Stelle stehen? Oder rollt es rückwärts?

Auflösung: Zehnstellige Primzahl gesucht

Veröffentlicht am von

Meine letzte Aufgabe dürfte manchem kaum lösbar erschienen sein:

Finden Sie alle zehnstelligen Primzahlen, die aus den Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 gebildet werden und jede dieser Ziffern genau einmal enthalten.

Aber wie oft bei derartigen Rätseln, ist die Lösung dann doch ziemlich einfach. Wenn es tatsächlich zehnstellige Primzahlen gibt, die diese Bedingung erfüllen, wie soll man die dann finden? Die letzte Ziffer muss ungerade sein, das ist klar. Aber wie prüft man dann, ob eine x-beliebige Zahlenkombination nun mehr als zwei Teiler hat? (Eine Primzahl ist nur durch 1 und sich selbst teilbar.)

Da ist es schon wahrscheinlicher, dass es keine einzige Zahl gibt, die eine Primzahl ist. Und das ist tatsächlich der Fall, denn jede aus den zehn Ziffern gebildete Zahl hat die Quersumme 45 und ist deshalb durch 3 teilbar.

Gestohlene Fahrräder online wiederfinden

Veröffentlicht am von

Fast 1000 Fahrräder werden in Deutschland jeden Tag geklaut. Die Polizei kann aber nur etwa jeden zehnten Raddiebstahl aufklären. Dass heißt: Neun von zehn Rädern bleiben verschollen – und die Diebe unerkannt. Die Polizei kommt ansonsten bei Diebstählen übrigens auf eine Aufklärungsquote von 30 Prozent – Fahrräder liegen mit 10 Prozent deutlich unterm Schnitt (Statistik: ADFC).

Erstaunlicherweise sind die Aufklärungsquoten von Ort zu Ort sehr verschieden. Neubrandenburg kommt laut geld.de-Studie auf 51 Prozent, Magdeburg auf 29 Prozent und München auf 22 Prozent. Hingegen liegen Hamburg und Berlin nur bei 4 Prozent, Potsdam sogar nur bei 3 Prozent.

Wenn die Polizei uns nicht hilft, helfen wir uns selbst – so entstand die Idee, gestohlene Bikes via Internet zu suchen. Für einige Schlagzeilen hat kürzlich der Rostocker Anbieter fahrradjaeger.de gesorgt. Firmengründer Martin Jäger hat nach eigener Aussage in sechs Semestern bereits fünf Rennräder eingebüßt. Nun sammelt er gemeinsam mit zwei Mitstreitern Diebstahlmeldungen.

Geld verdienen will er mit Aufklebern, die Diebe abschrecken sollen. Sie kosten 5 bzw. 9 Euro. Die teurere Variante hat einen QR-Code. Weil es auch Apps für iOS und Android, kann man diese QR-Codes mit einem Handy direkt am Rad auslesen.  So man erfährt sofort, ob das Rad vor einem evtl. als gestohlen gemeldet ist. Radfahrer – so die Idee – sollen selbst Ausschau halten nach verdächtigen Rädern, die womöglich gestohlen sind und mit der App prüfen, ob dies der Fall ist.

Bildquelle: fahrradjaeger.de

Wer einen Aufkleber möchte, registriert sein Rad auf der Webseite. Man kann sein  Rad bei fahrradjaeger.de aber auch als gestohlen melden, wenn es vor dem Diebstahl nicht registriert war. Das kostet bislang auch nichts.

Ich habe bei einer kurzen Recherche noch mehrere ähnliche Anbieter entdeckt: fahrrad-gestohlen.de (knapp 900 gestohlene Räder in der Datenbank), Fahrrad-Fahndung (rund 220 Räder) und Fahrrad-Fundbüro (nur 9 Räder). Bei fahrradjaeger.de umfasst die Datenbank als geklaut gemeldeter Drahtesel nach meiner Zählung rund 680 Stück. Nimmt man alle vier Anbieter zusammen, kommt man also auf 1800 als gestohlen gemeldete Räder.

Das sind angesichts der mehr als 300.000 verschwundenen Bikes pro Jahr gerade mal 0,6 Prozent. Der Anteil dürfte in Wahrheit noch kleiner sein, weil ein Teil der online gesammelten Diebstähle nicht in 2012, sondern in die Vorjahre fällt. Statistisch gesehen sind die Chancen also nach wie vor deutlich größer, dass die Polizei das Rad wiederfindet – zumindest in den Städten, wo sie ernsthaft ermittelt.

Aber die Idee der Datenbank im Netz finde ich auf jeden Fall gut. Wenn nur genügend Leute mitmachen – warum nicht auch Fahrradhändler? – könnte das wirklich funktionieren und auch den Dieben den Wiederverkauf erschweren.

Zehnstellige Primzahlen gesucht

Veröffentlicht am von

Ich habe ein neues Matherätsel für die Woche: Finden Sie alle zehnstelligen Primzahlen, die aus den Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 gebildet werden und jede dieser Ziffern genau einmal enthalten.

Ich bin Ihnen noch die Auflösung der Kopfnuss aus der vorigen Woche schuldig – ein klassisches Logikrätsel. Es ging um zehn Kinder, denen man kleine farbige Zettel auf die Stirn geklebt hat, entweder gelbe oder rote. Die Kinder können die Farbe ihres eigenen Zettels selbst nicht erkennen und dürfen weder miteinander reden noch sich anderweitig austauschen. Der Spielleiter sagt ihnen: „Fünf von euch haben einen roten Zettel auf der Stirn. Alle mit rotem Zettel sollen sofort zu mir kommen.“ Wenige Sekunden später sind die fünf Kinder bei ihm. Wie haben sie das angestellt?

Die Lösung ist nicht allzu schwer. Die Kinder wissen, dass fünf von ihnen rote Zettel auf der Stirn haben. Ein Kind, dass nur vier andere Kinder mit einem roten Zettel sieht, weiß daher, dass es selbst einen roten Zettel haben muss und geht schnell zum Spielleiter.

Kopfnuss der Woche: Sticker auf der Stirn

Veröffentlicht am von

Ich habe noch einen Nachschlag zu meinem Logik-Quiz. Die Aufgabe ist nicht besonders schwer, sie ist eine einfachere Variante von Frage 4. Ich habe sie auch schon mit Drittklässlern ausprobiert in der Knobel-AG, die ich seit September an der Schule meiner Tochter leite. Die Schüler haben sie souverän gemeistert. Hier das Rätsel:

Zehn Kinder bekommen kleine farbige Zettel auf die Stirn geklebt, entweder gelbe oder rote. Sie können die Farbe ihres eigenen Zettels selbst nicht erkennen und dürfen weder miteinander reden noch sich anderweitig austauschen. Der Spielleiter sagt ihnen: „Fünf von euch haben einen roten Zettel auf der Stirn. Alle mit rotem Zettel sollen sofort zu mir kommen.“ Wenige Sekunden später sind die fünf Kinder bei ihm. Wie haben sie das angestellt?

Wenn Sie Probleme haben, die Aufgabe zu durchschauen, empfehle ich Ihnen, erst einmal den Fall zu nehmen, dass nur einer der zehn Zettel rot ist.

Ein paar Erläuterungen zum Logik-Quiz auf SPON

Veröffentlicht am von

Heute ist auf SPIEGEL ONLINE ein Logik-Quiz von mir erschienen, zu dem ich viele Kommentare und Fragen per Mail bekommen habe. Viele Lesern meinten, in der Frage 2 (die mit den Berlinern) beziehungsweise in der Antwort dazu sei ein Fehler. Als ich die Mails las, dachte ich das im ersten Moment auch.

Der Kritikpunkt war folgender:  Die Verteilung, bei der sich in allen drei Tüten je ein Berliner mit Marmelade und einer mit Senf befindet, sei gar nicht berücksichtigt und deshalb könne die Antwort nicht stimmen. Im Aufgabentext steht:

„Bei KEINER der drei Tüten stimmt die Beschriftung mit dem Inhalt überein.“

Wenn in allen drei Tüten Marmelade + Senf drin wäre, dann auch in der
Tüte, auf der Marmelade + Senf steht. Das darf aber laut Aufgabe nicht
sein, denn dort steht, dass die Beschriftung bei allen drei Tüten
falsch ist. Daher ist diese Verteilung gar nicht möglich und muss
deshalb auch nicht berücksichtigt werden.

Kritik von drei oder vier Lesern gab es an einer Formulierung in Frage 1. Es geht um Bernds Aussage:

„Genau zwei von uns wollen ein Bier.“

Das ist zugegebenermaßen salopp formuliert. Man könnte das nämlich so verstehen, dass zwei sich ein Bier teilen wollen, was natürlich nicht gemeint war. An dieser Stelle merkt man wohl, dass ich nicht Mathematik, sondern Physik studiert habe! Präziser wäre die Formulierung gewesen:

„Genau zwei von uns wollen je ein Bier.“

Das ist die Sprache der Mathematiker und Logiker. Ich verspreche, mich zu bessern. Aber dann möglichst mit Formulierungen, die wenig formal klingen und trotzdem nicht falsch zu verstehen sind.

Ein paar Fragen gab es noch zur Frage 5, in der es um drei zum Tode verurteilte Männer geht. Die Männer können ihr Leben retten, wenn sich derjenige beim Richter meldet, der eine weiße Mütze trägt. Ich gehe bei der Aufgabe davon aus, dass alle drei Männer gute Logiker sind und nicht lange überlegen müssen, ob sie nun sagen „Ich hab die Mütze“ oder ob sie schweigen. Das steht aber nicht im Aufgabentext. Wenn der Mann ganz hinten zu lange überlegt, obwohl er selbst die weiße Mütze hat, könnte der vor ihm stehende tatsächlich denken, er selbst habe sie, weil er vor sich eine schwarze Mütze sieht und der Mann hinter ihm nichts sagt. Ganz ähnlich ist die Situation für den Mann ganz vorn. Beide müssen also erst mal ein Weilchen warten, bevor sie den Mund aufmachen. Sofern alle gute Logiker sind, reichen aber nur ein paar Sekunden – und dann sollte derjenige Bescheid wissen, der die weiße Mütze hat.

Ich hoffe, das trotzdem alle Spaß beim Rätseln hatten. Mir hat die U-Bahn-Aufgabe und die von der Lügner-Insel am besten gefallen.

Großer Spaß: Tweed Day Berlin 2012

Veröffentlicht am von

Cycling with a little bit of style – nun schon zum zweiten Mal in Berlin. Und ich war dieses Jahr endlich auch dabei. Etwa 70, 80 Leute waren am Sonntagmittag zum Gendarmenmarkt gekommen, um dann über Mitte und Tiergarten nach Charlottenburg zu radeln. Keine Frage, der Tweed Run in London ist deutlich größer. Aber die Stimmung ist bei beiden Tweed-Rundfahrten ganz ähnlich. Gut gelaunte Menschen treffen sich, um gemeinsam durch eine Stadt zu rollen. Es hat großen Spaß gemacht – vielen Dank an die Organisatoren des Tweed Day Berlin! Am Schloss Charlottenburg war Tea Time, dann gab’s am Kudamm Gin – und am Ende wurden in einem Irish Pub Preise verteilt. Das Tempo war übrigens sehr gemütlich, mir eigentlich eine Spur zu langsam. Aber so hatten wir wenigstens genug Zeit, um einander kennenzulernen. Ich weiß seit heute, dass mir zum Fahrradnerd noch so einiges fehlt – unter anderem das eine oder andere Rad.

Fotos: Copyright Holger Dambeck

So parkt man in Malmö

Veröffentlicht am von

Manchmal muss man das Offensichtliche noch mal extra deutlich zeigen – so wie in Malmö. In einer Straße im Zentrum habe ich diesen Fahrradabstellplatz entdeckt. Wo normalerweise ein Auto parkt, stehen nun bis zu acht Fahrräder. Solange genug Platz auf den Fußwegen zum Abstellen der Räder ist, muss man sowas natürlich nicht machen. Aber in Radmetropolen wie Kopenhagen oder dem gegenüberliegenden Malmö reicht der Raum oft einfach nicht.

Die anderen beiden Fotos zeigen eine Gratis-Tiefgarage für Velos in Amsterdam und eine Garage für Cargo-Bikes in Kopenhagen. In der dänischen Hauptstadt sind die dreirädrigen Christiania-Bikes und Niholas weit verbreitet und auch ein beliebtes Klauobjekt. Damit die sperrigen Transporträder nachts sicher stehen, hat die Stadt eine solche autoförmige Garage gebaut. Mikael Colville-Andersen hatte mich bei meinem  Kopenhagen-Besuch Anfang 2011 zu dem Mini-Parkhaus geführt. Er ist auf dem Foto rechts zu sehen.

 

Die wahre Olympia-Medaillenstatistik

Veröffentlicht am von

Olympia 2012 ist Geschichte. Ich habe noch mal ein bisschen mit der Medaillenstatistik gespielt. Normalerweise zählt allein Gold – oder man zählt alle drei Medaillen zusammen. Das kommt dabei heraus (To-10 Gold):

Platz                        Gold  Silber Bronze          Summe Medaillen
1. USA                     46   29   29                       104
2. China                  38   27   22                        87
3. Großbritannien    29   17   19                       65
4. Russland             24   25   33                       82
5. Südkorea            13   8      7                         28
6. Deutschland       11   19   14                        44
7. Frankreich          11   11   12                        34
8. Italien                    8    9    11                        28
9. Ungarn                 8    4     5                         17
10. Australien           7    16   12                       35

Besonders fair ist das natürlich nicht. Deutschland hatte ja bekanntlich besonders viele Silbermedaillen. Deshalb habe ich die Medaillen zuerst einmal gewichtet. Gold sind drei Punkte, Silber zwei und Bronze einer. In einem zweiten Schritt habe ich die Medaillen dann noch in Bezug zur Einwohnerzahl gestellt. Schließlich würde man ja erwarten, dass es in einem großen Land auch mehr Talente gibt – und bei gleicher Sportförderung entsprechend mehr Medaillen. Was kommt dabei heraus?

Die Gewichtung der Medaillen (Gold: 3 Punkte, Silber 2 usw.) ändert erstaunlicherweise  kaum etwas an den Top-10. Im Vergleich zur Gold-Statistik rutscht Deutschland einen Platz vor, das mit viel Gold, aber vergleichsweise wenig Silber und Bronze dekorierte Südkorea fällt zurück.

Interessanter ist da schon die Medaillen-Statistik pro eine Million Einwohner. Sie wird angeführt von kleinen Ländern wie Grenada (100.000 Einwohner), Bahamas (300.000) und Jamaika (3 Millionen). Erstaunlich finde ich, dass Neuseeland, Australien, Ungarn und Dänemark (in der gewichteten 312-Medaillenstatistik) so weit oben rangieren. Dort funktioniert die Talenteförderung offenbar viel besser – bzw. man fokussiert sich auf bestimmte Sportarten, wo dann viele Medaillen geholt werden. Bezogen auf die Einwohnerzahl liegt Deutschland im oberen Drittel: Rang 30 mit 0,135 Goldmedaillen pro Millionen Einwohner, die USA sind mit 0,147 nur zwei Plätze weiter vorn. In der gewichteten Medaillenstatistik (321) liegt Deutschland (33.) sogar vor den USA (46).

Die Medaillenstatistik stammt von SPIEGEL ONLINE, die Einwohnerzahlen habe ich aus dem CIA World Factbook übernommen.